第三章

P78:3.3.2.(1)(中文版厚书)

由 a 和 b 两个字母组成的, 首尾皆为 a 的任意长度大于等于 2 的字符串.

P79:3.3.5.(1)(中文版厚书)

aa∗ee∗ii∗oo∗uu∗aa^*ee^*ii^*oo^*uu^*

P96:3.6.3(中文版厚书)

  • 0 -> 1 -> 2 -> 2 -> 3
  • ?

不需要保证所有路径都可以接受, 所以 0 -> 1 -> 2 -> 2 -> 3 和 0 -> 1 -> 1 -> 1 -> 1 均可.

P96:3.6.5.(1)(中文版厚书)

a b
0 {0,1} {0}
1 {1,2} {1}
2 {0,1,2} {0,2,3}
3 0\cancel{0} 0\cancel{0}

需要严格按照 NFA 中的结构, 所以不能跳过 ϵ\epsilon, 应该改为如下形式:

a b ϵ\epsilon
0 {0,1} {0} 0\cancel{0}
1 {1,2} {1} 0\cancel{0}
2 {2} {2,3} {0}
3 0\cancel{0} 0\cancel{0} 0\cancel{0}

P105:3.7.1.(2)(中文版厚书)

首先将 NFA 转化为 DFA, 得到 DFA 如下:

DFA 0 0 0->0 b 0, 1 0, 1 0->0, 1 a 0, 1->0, 1 b 0, 1, 2 0, 1, 2 0, 1->0, 1, 2 a 0, 1, 2->0, 1, 2 a 0, 1, 2, 3 0, 1, 2, 3 0, 1, 2->0, 1, 2, 3 b 0, 1, 2, 3->0, 1, 2 a 0, 1, 2, 3->0, 1, 2, 3 b
DFA

令 0 = A, “0, 1” = B, “0, 1, 2” = C, “0, 1, 2, 3” = D, 尝试划分不同的状态集:

  1. {D}, {A, B, C}
  2. {D}, {C}, {A, B}
  3. {D}, {C}, {B}, {A}

则原来的 DFA 已经是最简.

第四章作业

P130:4.2.1(中文版厚书)

1)

S→SS∗→SS+S∗→aS+S∗→aa+S∗→aa+a∗S \to SS* \to SS+S* \to aS+S* \to aa+S* \to aa+a*

2)

S→SS∗→Sa∗→SS+a∗→Sa+a∗→aa+a∗S \to SS* \to Sa* \to SS+a* \to Sa+a* \to aa+a*

3)

语法分析树 A S B S A->B C S A->C D * A->D E S B->E F S B->F G + B->G H a C->H I a E->I J a F->J
语法分析树

5)

包含加法和乘法的关于a的后缀表达式

P147:4.4.1.(6)(中文版厚书)

设 bexpr = E, bterm = T, bfactor = F, 则消除左递归后的文法如下:

E→TE′E′→orTE′∣ϵT→FT′T′→andFT′∣ϵF→notF∣(E)∣true∣falseE \to TE' \\ E' \to or T E' | \epsilon \\ T \to FT' \\ T' \to and F T' | \epsilon \\ F \to not F | (E) | true | false

有时候不只需要要消除左递归, 还要提取左公因子

First 集合如下:

First(F)=First(T)=First(E)=not,(,true,falseFirst(T′)=and,ϵFirst(E′)=or,ϵFirst(F) = First(T) = First(E) = {not, (, true, false} \\ First(T') = {and, \epsilon} \\ First(E') = {or, \epsilon}

Follow 集合如下:

Follow(E)=Follow(E′)=$,)Follow(T)=Follow(T′)=or,$,)Follow(F)=and,or,$,)Follow(E) = Follow(E') = {\$, )} \\ Follow(T) = Follow(T') = {or, \$, )} \\ Follow(F) = {and, or, \$, )}

注意 First 集合中可以出现 ϵ\epsilon , 但是 Follow 集合中不行

预测分析表如下:

非终结符 or and not ( ) true false $
E E→TE′E\to TE' E→TE′E\to TE' E→TE′E\to TE' E→TE′E\to TE'
E’ E′→orTE′E' \to or T E' E′→ϵE' \to \epsilon E′→ϵE' \to \epsilon
T T→FT′T \to FT' T→FT′T \to FT' T→FT′T \to FT' T→FT′T \to FT'
T’ T′→ϵT' \to \epsilon T′→andFT′T' \to and F T' T′→ϵT' \to \epsilon T′→ϵT' \to \epsilon
F F→notFF\to not F F→(E)F\to (E) F→trueF\to true F→falseF\to false

P147:4.4.4.(3)(中文版厚书)

First(S)=(Follow(S)=)First(S) = {(}\\ Follow(S) = {)}

漏掉了 ϵ\epsilon 和 $\$, 答案应该是:

First(S)=(,ϵFollow(S)=),$First(S) = {(, \epsilon}\\ Follow(S) = {), \$}

P147:4.4.5.(1)(中文版厚书)

浪费了我非常多时间, 一直百思不得其解这里的逻辑会有什么问题…最后查了很多帖子才发现这里的问题主要出现在代码实现上…具体可以参考这个解答 https://stackoverflow.com/a/49465845. 问题的关键在于, 递归下降法的代码中, 只会在失配的地方进行回溯, 从而导致了错误, 事实上发生错误的地方早在发生失配之前.
观察展开得到的形如"aa…aaSaa…aa"的字符串, 第一次失配的时候, 中间的 “aSa” 会变成 “aa”, 总共会减少 0 个 a; 以此类推(注意只会在发生失配的地方回溯), 截止到第二次失配后, 总共会减少 2 个 a; 截止到第三次失配后, 总共会减少 4 个 a… 假设待识别串的长度为 n, 为了让最终字符串能识别成功, 需要要满足 2∗n−2k−1=n2*n - 2^{k - 1} = n, 其中 k 为失配次数. 则 n 需要是 2 的幂.

P153:4.5.2.(3)(中文版厚书)

  • a aa*a++: S -> a
  • Sa a*a++: S -> a
  • SSa *a++: S -> a
  • SSS* a++: S -> SS*
  • SSa ++: S -> a
  • SSS+ +: S -> SS+
  • SS+: S -> SS+

P153:4.5.3.(2)(中文版厚书)

将上述过程画成树形图即可, 略.

P164:4.6.2(中文版厚书)

给文法编号如下:

S→SS+(1)S→SS∗(2)S→a(3) S\to SS+ (1) \\ S\to SS* (2) \\ S\to a (3)

First(S)=aFollow(S)=a,∗,+ First(S) = {a} \\ Follow(S) = {a, *, +}

不同的状态集如下:

I0:S′→.S,S→.SS+,S→.SS∗,S→.aI_0: S'\to .S, S\to .SS+, S\to .SS*, S\to .a
I1:S′→S.,S→S.S+,S→S.S∗,S→.SS+,S→.SS∗,S→.aI_1: S'\to S., S\to S.S+, S\to S.S*, S\to .SS+, S\to .SS*, S\to .a
I2:S→a.I_2: S\to a.
I3:S→SS.+,S→SS.∗,S→S.S+,S→S.S∗,S→.aI_3: S\to SS.+, S\to SS.*, S\to S.S+, S\to S.S*, S\to .a
I4:S→SS+.I_4: S\to SS+.
I5:S→SS∗.I_5: S\to SS*.
I6:S→SS.+,S→SS.∗I_6: S\to SS.+, S\to SS.*

构造的语法分析表如下:

状态 + * a $ S
0 s2 1
1 s2 acc 3
2 r3 r3 r3
3 s4 s5 s2 6
4 r1 r1 r1
5 r2 r2 r2
6 s4 s5

没有发现冲突, 故是 SLR 文法.

首先在给文法排序的时候漏写了增广文法(虽然编号没错), 然后Follow集求错了, 最后状态集有错, 修改后如下:

给文法编号如下:

S′→S(0)S→SS+(1)S→SS∗(2)S→a(3) S'\to S (0) \\ S\to SS+ (1) \\ S\to SS* (2) \\ S\to a (3)

First(S)=aFollow(S′)=$First(S)=aFollow(S)=a,∗,+,$ First(S) = {a} Follow(S') = {\$} \\ First(S) = {a} \\ Follow(S) = {a, *, +, \$}

不同的状态集如下:

I0:S′→.S,S→.SS+,S→.SS∗,S→.aI_0: S'\to .S, S\to .SS+, S\to .SS*, S\to .a
I1:S′→S.,S→S.S+,S→S.S∗,S→.SS+,S→.SS∗,S→.a,S→.SS+,S→.SS∗I_1: S'\to S., S\to S.S+, S\to S.S*, S\to .SS+, S\to .SS*, S\to .a, S\to .SS+, S\to .SS*
I2:S→a.I_2: S\to a.
I3:S→SS.+,S→SS.∗,S→S.S+,S→S.S∗,S→.a,S→.SS+,S→.SS∗I_3: S\to SS.+, S\to SS.*, S\to S.S+, S\to S.S*, S\to .a, S\to .SS+, S\to .SS*
I4:S→SS+.I_4: S\to SS+.
I5:S→SS∗.I_5: S\to SS*.

构造的语法分析表如下:

状态 + * a $ S
0 s2 1
1 s2 acc 3
2 r3 r3 r3 r3
3 s4 s5 s2 3
4 r1 r1 r1 r1
5 r2 r2 r2 r2

没有发现冲突, 故是 SLR 文法.

P164:4.6.3(中文版厚书)

栈 符号 输入 动作
0 aa*a+$ 移入
02 a a*a+$ 根据 S -> a 规约
01 S a*a+$ 移入
012 Sa *a+$ 根据 S -> a 规约
013 SS *a+$ 移入
0135 SS* a+$ 根据 S -> SS* 规约
01 S a+$ 移入
012 Sa +$ 根据 S -> a 规约
013 SS +$ 移入
0134 SS+ $ 根据 S -> SS+ 规约
01 S $ acc

P165:4.6.6(中文版厚书)

尝试 LL(1).

首先消除左递归, 得到如下文法:

S→AS′S′→AS′∣ϵA→a S\to AS' \\ S'\to AS' | \epsilon \\ A\to a

求 First 集合如下:

A:aS:aS′:a,ϵ A: {a} \\ S: {a} \\ S': {a, \epsilon}

求 Follow 集合如下:
S:$S′:$A:$,a S: { \$ } \\ S': {\$} \\ A: {\$, a} \\

构造预测分析表如下:

非终结符 a $
S S→AS′S\to AS'
S S′→AS′S'\to AS' S′→ϵS'\to \epsilon
A A→aA\to a

这类题不能消除左递归, 只能使用原文法进行判断, 所以正确答案如下:

S -> SA 和 S -> A 均能推导出以 a 开头的字符串, 所以文法不是 LL(1) 的.

尝试使用 SLR(1) 文法.

对文法进行增广并排序如下:

S′→S(0)S→SA(1)S→A(2)A→a(3) S'\to S (0)\\ S\to SA (1) \\ S\to A (2) \\ A\to a(3)

划分状态集如下:

I0=S′→.S,S→.SA,S→.A,A→.aI1=S′→S.,S→S.A,A→.aI2=S→A.I3=A→a.I4=S→SA. I_0 = S' \to .S, S \to .SA, S\to .A, A\to .a \\ I_1 = S' \to S., S\to S.A, A\to .a \\ I_2 = S\to A. \\ I_3 = A\to a. \\ I_4 = S\to SA.\\

GOTO(0,S)=1GOTO(0,A)=2GOTO(1,A)=4 GOTO(0, S) = 1 \\ GOTO(0, A) = 2 \\ GOTO(1, A) = 4\\

First(A)=aFirst(S)=aFirst(S′)=a First(A) = a\\ First(S) = a\\ First(S') = a

$
Follow(S’) = $\
Follow(S) = $, a\
Follow(A) = ,a, a

构造出的语法分析表为:

状态 a $ S A
0 s3 1 2
1 s3 acc 4
2 r2 r2
3 r3 r3
4 r1 r1

没有冲突, 故文法是 SLR 的.

P177:4.7.1(中文版厚书)

对文法进行增广并排序, 得到:

S′→S(0)S→SS+(1)S→SS∗S→a S'\to S(0)\\ S\to SS+(1)\\ S\to SS*\\ S\to a

First(S)=aFisst(S′)=a First(S) = a\\ Fisst(S') = a

Follow(S′)=$Follow(S)=$,a Follow(S') = \$\\ Follow(S) = \$, a

划分 规范LR 状态集族如下:

I0=S′→.S,$;S→.SS+,$/a;S→.SS∗,$/a;S→.a,$/aI1=S′→S.,$;S→S.S+,$/a;S→S.S∗,$/a;S→.SS+,+/∗/a;S→.SS∗,+/∗/a;S→.a,+/∗/aI2=S→SS.+,$/a;S→SS.∗,$/a;S→S.S+,+/∗/a;S→S.S∗,+/∗/a;S→.SS+,+/∗/a;S→.SS∗,+/∗/a;S→.a,+/∗/aI3=S→SS.+,+/∗/a;S→SS.∗,+/∗/a;S→S.S+,+/∗/a;S→S.S∗,+/∗/a;S→.SS+,+/∗/a;S→.SS∗,+/∗/a;S→.a,+/∗/a;I4=S→a.,$/aI5=S→a.,+/∗/aI6=S→SS+.,$/aI7=S→SS+.,+/∗/aI8=S→SS∗.,$/aI9=S→SS∗.,+/∗/a I_0 = S'\to .S, \$; S\to .SS+, \$/a; S\to .SS*, \$/a; S\to .a, \$/a\\ I_1 = S'\to S., \$; S\to S.S+, \$/a; S\to S.S*, \$/a; S\to .SS+, +/*/a; S\to .SS*, +/*/a; S\to .a, +/*/a\\ I_2 = S\to SS.+, \$/a; S\to SS.*, \$/a; S\to S.S+, +/*/a; S\to S.S*, +/*/a; S\to .SS+, +/*/a; S\to .SS*, +/*/a; S\to .a, +/*/a\\ I_3 = S\to SS.+, +/*/a; S\to SS.*, +/*/a; S\to S.S+, +/*/a; S\to S.S*, +/*/a; S\to .SS+, +/*/a; S\to .SS*, +/*/a; S\to .a, +/*/a;\\ I_4 = S\to a., \$/a\\ I_5 = S\to a., +/*/a\\ I_6 = S\to SS+., \$/a\\ I_7 = S\to SS+., +/*/a\\ I_8 = S\to SS*., \$/a\\ I_9 = S\to SS*., +/*/a\\

划分 LALR 项集族如下:

I0=S′→.S,$;S→.SS+,$/a;S→.SS∗,$/a;S→.a,$/aI1=S′→S.,$;S→S.S+,$/a;S→S.S∗,$/a;S→.SS+,+/∗/a;S→.SS∗,+/∗/a;S→.a,+/∗/aI2=S→SS.+,+/∗/a/$;S→SS.∗,+/∗/a/$;S→S.S+,+/∗/a;S→S.S∗,+/∗/a;S→.SS+,+/∗/a;S→.SS∗,+/∗/a;S→.a,+/∗/a;I3=S→a.,+/∗/a/$I4=S→SS+.,+/∗/a/$I5=S→SS∗.,+/∗/a/$ I_0 = S'\to .S, \$; S\to .SS+, \$/a; S\to .SS*, \$/a; S\to .a, \$/a\\ I_1 = S'\to S., \$; S\to S.S+, \$/a; S\to S.S*, \$/a; S\to .SS+, +/*/a; S\to .SS*, +/*/a; S\to .a, +/*/a\\ I_2 = S\to SS.+, +/*/a/\$; S\to SS.*, +/*/a/\$; S\to S.S+, +/*/a; S\to S.S*, +/*/a; S\to .SS+, +/*/a; S\to .SS*, +/*/a; S\to .a, +/*/a;\\ I_3 = S\to a., +/*/a/\$\\ I_4 = S\to SS+., +/*/a/\$\\ I_5 = S\to SS*., +/*/a/\$\\

第五章作业

P198:5.1.2

产生式 语义规则
L→EnL\to En L.syn=E.synL.syn=E.syn
E→TE′E\to TE' E′.inh=T.syn,E.syn=E′.synE'.inh = T.syn, E.syn = E'.syn
E′→+TE1′E'\to +TE_1' E1′.inh=E′.inh+T.syn,E1′.syn=E1′.inhE_1'.inh = E'.inh+T.syn, E_1'.syn = E_1'.inh
E′→ϵE'\to \epsilon E′.syn=E.inhE'.syn = E.inh
T→FT′T\to FT' T′.inh=F.syn,T.syn=T′.synT'.inh = F.syn, T.syn = T'.syn
T′→+FT1′T'\to +FT_1' T1′.inh=T′.inh+F.syn,T1′.syn=T1′.inhT_1'.inh = T'.inh+F.syn, T_1'.syn = T_1'.inh
T′→ϵT'\to \epsilon T′.syn=T.inhT'.syn = T.inh
F→(E)F\to (E) F.syn=E.synF.syn = E.syn
F→digitF\to digit F.syn=digit.lexvalF.syn = digit.lexval

注意E, F等非左递归产生的中间符号只有val属性, 而且上面的表格中还包含了一些小错误, 调整后如下:

产生式 语义规则
L→EnL\to En L.val=E.valL.val=E.val
E→TE′E\to TE' E′.inh=T.val,E.val=E′.synE'.inh = T.val, E.val = E'.syn
E′→+TE1′E'\to +TE_1' E1′.inh=E′.inh+T.val,E′.syn=E1′.synE_1'.inh = E'.inh+T.val, E'.syn = E_1'.syn
E′→ϵE'\to \epsilon E′.syn=E′.inhE'.syn = E'.inh
T→FT′T\to FT' T′.inh=F.val,T.val=T′.synT'.inh = F.val, T.val = T'.syn
T′→∗FT1′T'\to *FT_1' T1′.inh=T′.inh∗F.val,T′.syn=T1′.synT_1'.inh = T'.inh*F.val, T'.syn = T_1'.syn
T′→ϵT'\to \epsilon T′.syn=T′.inhT'.syn = T'.inh
F→(E)F\to (E) F.val=E.valF.val = E.val
F→digitF\to digit F.val=digit.lexvalF.val = digit.lexval

P202:5.2.2.(2)

格式可参考 https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch05/5.2/5.2.md#522

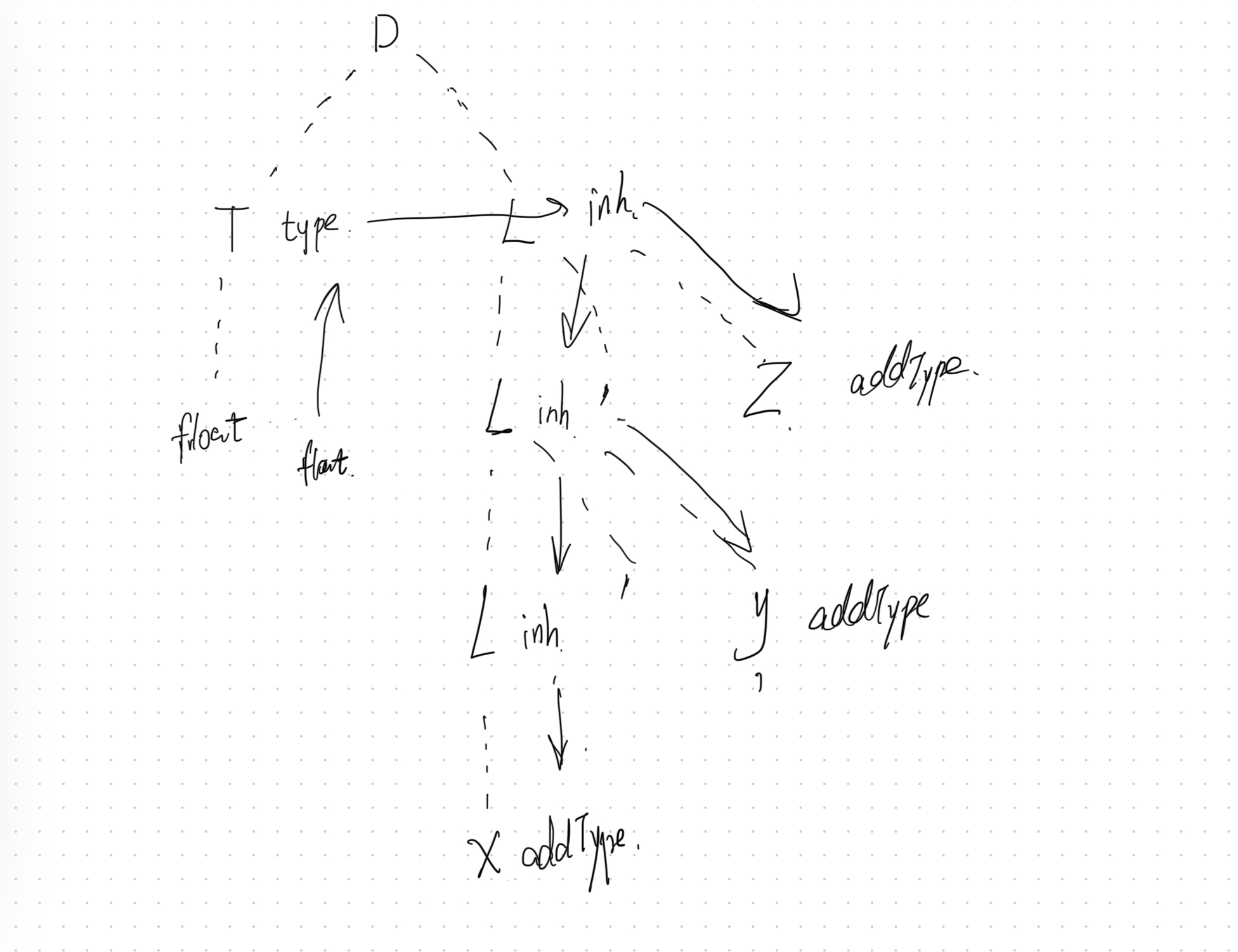
注释语法分析树

P216:5.4.3

消除左递归如下:

B→{B.val=B′.syn}1B′{B′.inh=1}B′→{B′.sys=B1′.sys}CB1′{B1′.inh=B′.inh∗2+C.val}B′→{B′.sys=B′.inh}ϵC→0{C.val=0}C→1{C.val=1} B\to \{B.val = B'.syn\}1B' \{B'.inh = 1\} \\ B'\to \{B'.sys = B_1'.sys\}CB_1'\{B_1'.inh = B'.inh * 2 + C.val\} \\ B'\to \{B'.sys = B'.inh\}\epsilon \\ C\to 0\{C.val = 0\}\\ C\to 1\{C.val = 1\}

注意 SDT 动作的位置, inh 属性的更新动作要在符号的左边, sys 属性的更新要在符号的右边, 更改后如下:

B→1{B′.inh=1}B′{B.val=B′.syn}B′→C{B1′.inh=B′.inh∗2+C.val}B1′{B′.syn=B1′.syn}B′→ϵ{B′.syn=B′.inh}C→0{C.val=0}C→1{C.val=1} B\to 1\{B'.inh = 1\}B' \{B.val = B'.syn\}\\ B'\to C\{B_1'.inh = B'.inh * 2 + C.val\}B_1'\{B'.syn = B_1'.syn\} \\ B'\to \epsilon\{B'.syn = B'.inh\} \\ C\to 0\{C.val = 0\}\\ C\to 1\{C.val = 1\}

第六章作业

P232:6.1.2

DAG

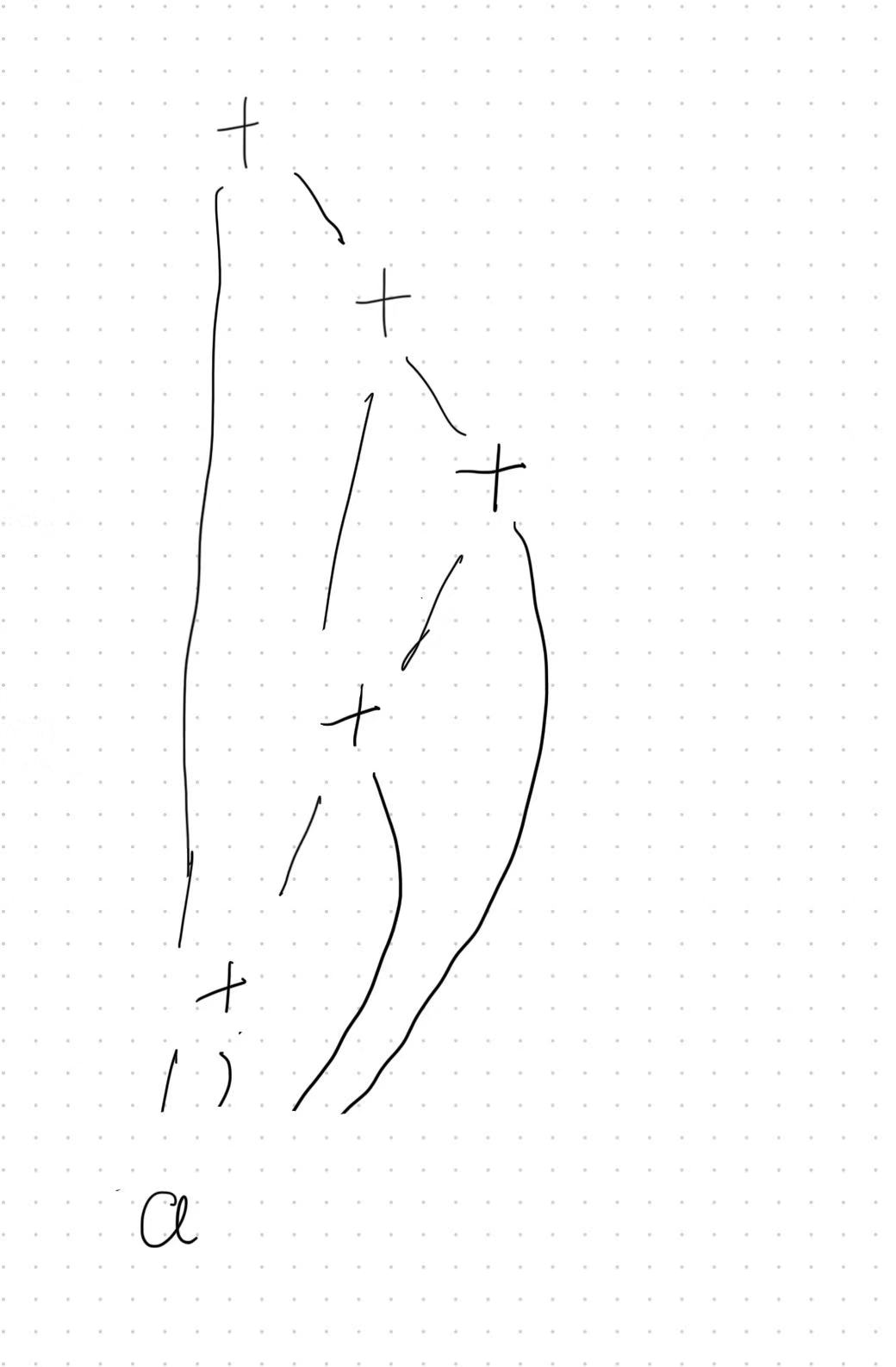
"子表达式的值编码"似乎并未在 PPT 中被提及, 可以参考 https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch06/6.1/6.1.md#解答-1

P225:6.2.2

1)

四元式序列:

序号 op arg1arg_1 arg2arg_2 result
0 ×\times i 8 i’
1 + b i’ t1t_1
2 * t1t_1 x1x_1
3 ×\times j 8 j’
4 + c j’ t2t_2
5 * t2t_2 x2x_2
6 + x1x_1 x2x_2 a

三元式序列:

序号 op arg1arg_1 arg2arg_2
0 ×\times i 8
1 + b (0)
2 * (1)
3 ×\times j 8
4 + c (3)
5 * (4)
6 + (2) (5)
7 = a (6)

2)

同 1), 略.

P247:6.4.3.(3)

Laddr1=i∗16t1=j∗4Laddr2=Laddr1+t1Eaddr1=b[Laddr2]Laddr3=Eaddr1∗12Laddr4=k∗4Eaddr2=c[Laddr4]t2=Eaddr2∗4Laddr5=Laddr3+t2Eaddr3=a[Laddr5]x=Eaddr3 Laddr_1 = i * 16\\ t_1 = j * 4\\ Laddr_2 = Laddr_1 + t_1\\ Eaddr_1 = b[Laddr_2]\\ Laddr_3 = Eaddr_1 * 12\\ Laddr_4 = k * 4\\ Eaddr_2 = c[Laddr_4]\\ t_2 = Eaddr_2 * 4\\ Laddr_5 = Laddr_3 + t_2 \\ Eaddr_3 = a[Laddr_5] \\ x = Eaddr_3

这里的变量命名其实可以全部统一成 tit_i 的形式, 直接按照规约顺序编号即可, 可参考 https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch06/6.4/6.4.md#643

P248:6.4.8

水题, 略. 可参考 https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch06/6.4/6.4.md#648

P263:6.6.1

设产生式为:

S→S1S2 S\to S_1S_2

则语义规则为:

begin=newlabel()B.true=newlabel()B.false=S.nextS.code=S1.code∣∣label(begin)∣∣B.code∣∣label(B.true)∣∣S3.code∣∣S2.code∣∣gen(′goto′begin) begin = newlabel() \\ B.true = newlabel()\\ B.false = S.next\\ S.code = S_1.code || label(begin) || B.code || label(B.true) || S_3.code || S_2.code || gen('goto' begin)

注意每个子 S 都有 next 属性(本质上存了一个label)需要维护, 更改后如下:

begin=newlabel()S1.next=beginB.true=newlabel()B.false=S.nextS2.next=beginS3.next=newlabel()S.code=S1.code∣∣label(begin)∣∣B.code∣∣label(B.true)∣∣S3.code∣∣label(S3.next)∣∣S2.code∣∣gen(′goto′begin) begin = newlabel() S_1.next = begin B.true = newlabel()\\ B.false = S.next\\ S_2.next = begin \\ S_3.next = newlabel() \\ S.code = S_1.code || label(begin) || B.code || label(B.true) || S_3.code || label(S_3.next) || S_2.code || gen('goto' begin)

P268:6.7.1.(2)

a==b:truelist={100},falselist={101}c==d:truelist={102},falselist={103}e==f:truelist={104},falselist={105}(a==b∣∣c==d):truelist={100,102},falselist={103}(a==b∣∣c==d)∣∣e==f:truelist={100,102,104},falselist={105} a == b : truelist = \{100\}, falselist = \{101\}\\ c == d : truelist = \{102\}, falselist = \{103\}\\ e == f : truelist = \{104\}, falselist = \{105\}\\ (a == b || c == d) : truelist = \{100, 102\}, falselist = \{103\} \\ (a == b || c == d) || e == f : truelist = \{100, 102, 104\}, falselist = \{105\}

漏掉了一个表达式 a == b || c == d, 其与( a == b || c == d) 打结果一样, 也是 $truelist = {100, 102}, falselist = {103} $

第七章作业

P283:7.2.4

参考 https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch07/7.2/7.2.md#724

P303:7.5.2

D, F, G 的引用计数会变为 0

P311:7.6.1

参考 https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch07/7.6/7.6.md#answer

第八章作业

P333:8.2.2

1)

LD R1, i
MUL R1, R1, #4
LD R2, a(R1)
LD R3, j
MUL R3, R3, #4
LD R4, b(R3)
ST a(R1), R4
ST b(R3), R2

2)

LD R1, i
MUL R1, R1, #4
LD R2, a(R1)
LD R1, b(R1)
MUL R1, R2, R1
ST z, R1

P305:8.2.4

LD R1, x
LD R2, y
SUB R1, R1, R2
BLTZ R1, L1
LD R1, #0
ST z, R1
BR L2
L1: LD R1, #1
ST z, R1

P348:8.5.1

https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch08/8.5/8.5.md#851, 注意 d 和 b 需要合并

补充题目

DAG图

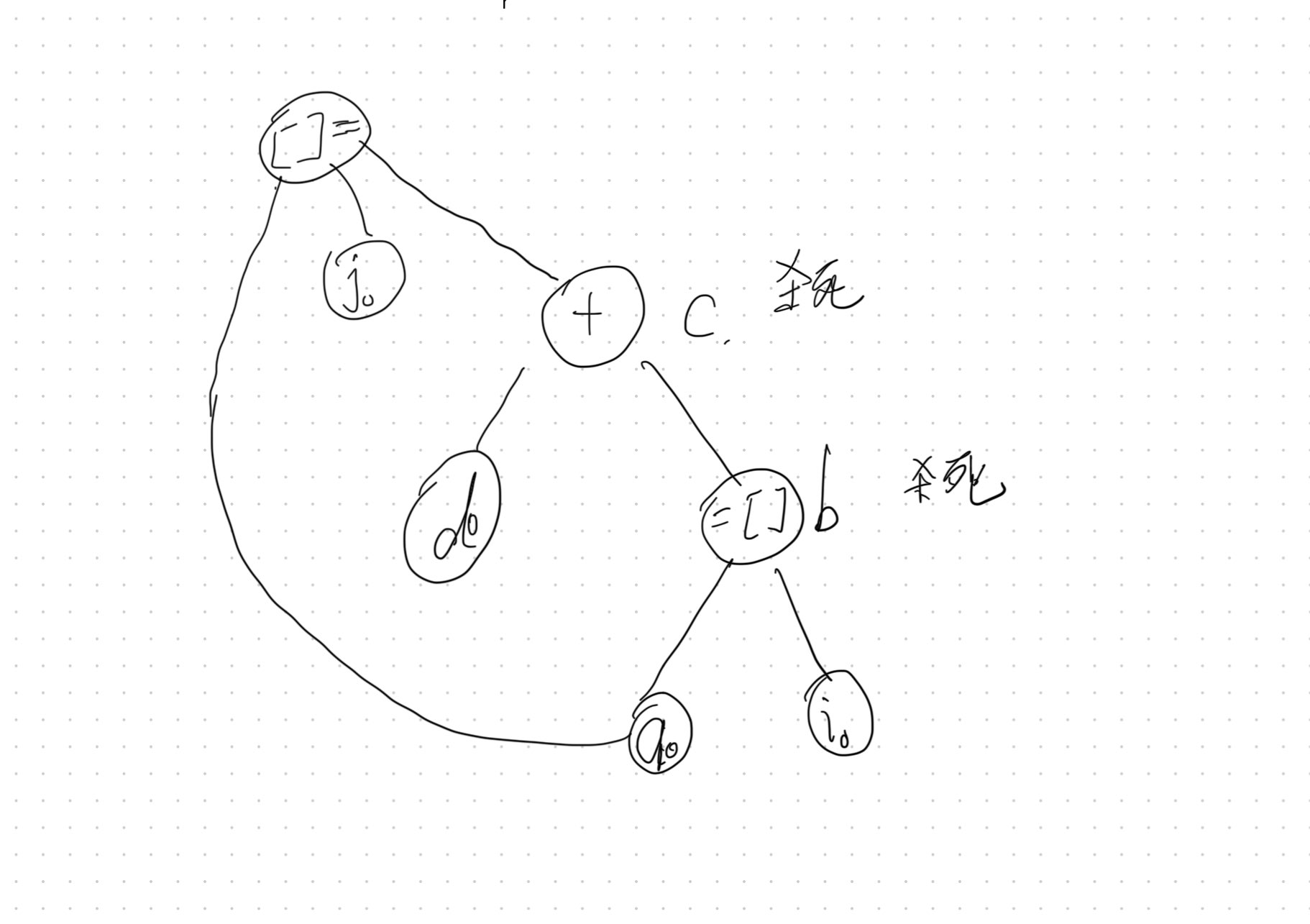
P352:8.6.1.(1)

t1 = b * c
t2 = a + t1
x = t2

P353:8.6.5.(1)

机器代码 R1 R2 a b c x t1 t2
LD R1, b b a b, R1 c
LD R2, c b c a b, R1 c, R2
MUL R1, R1, R2 t1 c a b c, R2 R1
LD R2, a t1 a a, R2 b c R1
ADD R1, R1, R2 t2 a a, R2 b c R1
ST x, R1 x, t2 a a, R2 b c x, R1 R1

第九章作业

P381:9.1.1 & P382:9.1.4

参考 https://blog.csdn.net/justice0/article/details/82701527

P394:9.2.1

1)

基本块 gen kill
B1 (1)(2)
B2 (3)(4) (5)
B3 (5) (4)(6)
B4 (6)(7) (5)(9)
B5 (8)(9) (2)(7)
B6 (10)(11) (1)(8)

2)

基本块 IN OUT
B1 (1)(2)
B2 (1)(2)(3)(5)(8)(9) (1)(2)(3)(4)(8)(9)
B3 (1)(2)(3)(4)(6)(7)(8)(9) (1)(2)(3)(5)(7)(8)(9)
B4 (1)(2)(3)(5)(7)(8)(9) (1)(2)(3)(6)(7)(8)
B5 (1)(2)(3)(5)(7)(8)(9) (1)(3)(5)(8)(9)
B6 (1)(3)(5)(8)(9) (3)(5)(9)(10)(11)

P394:9.2.3

基本块 def use
B1 a, b
B2 c, d a, b
B3 b, d
B4 d a, b, e
B5 e a, b, c
B6 a b, d
基本块 IN OUT
B1 e a, b, e
B2 a, b, e a, b, c, d, e
B3 a, b, c, d, e a, b, c, d, e
B4 a, b, c, e a, b, c, d, e
B5 a, b, c, d a, b, d
B6 b, d